

产品介绍
产 品 列 表
DFCD-Plasma
DFCD-Plasma是专用于预测物体形状在气-固界面处由于化学组分输运与表面反应共同作用而发生的变化仿真工具。由于气-固界面的形状和方向会影响反应物的输运,因此该预测需要求解一个包含移动界面、反应物输运,以及局部组分通量与反应速率之间平衡的瞬态问题。目前,组分输运分析仅限于在计算域长度尺度上的自由分子(即气相无碰撞)输运。因此,DFCD-Plasma最适用于预测通过气相过程(如化学气相沉积或等离子体增强刻蚀)向较小形貌特征沉积或从中刻蚀所产生的影响。
应用场景
DFCD-Plasma是为数值分析半导体工艺步骤对器件特征尺度的影响开发的。典型应用示例为:
- 预测通过化学气相沉积或等离子体增强化学气相沉积填充沟槽的过程,以判断沟槽是否完全填充或是否存在初始空洞;
- 分析施加的晶圆偏压及相应离子能量对刻蚀速率和轮廓形状的影响;
- 预测在已有结构中进行物理气相沉积薄膜时的覆盖情况。
基础理论
DFCD-Plasma采用水平集方法来定义模型中材料界面的位置,并实现界面随时间的移动。模型中每种固体材料均定义一个标量水平集函数,求解随时间变化的离散化水平集方程,原则上需要在整个计算域内获取这些函数的值。该计算域应包含原始材料边界以及它们在模拟过程中将要移动到的区域。显然,最关注的信息是水平集函数在材料界面附近区域的值。目前有多种方法可用于降低求解的计算量。采用规则的笛卡尔网格,识别出靠近零水平集的解节点带状区域,并仅对这些节点进行计算。这种带状区域方法需要额外的工作来持续判断网格中哪些节点应进入或离开工作区域,并在节点进入带状区域时适当地扩展水平集函数的值。DFCD-Plasma可采用自适应网格细化方法,在材料界面附近实现高分辨率的同时,降低远离界面区域的计算量。DFCD-Plasma中的分层自适应网格细化算法基于树型数据结构,使用笛卡尔单元。笛卡尔单元(即各面与主坐标轴对齐的六面体)的使用,使得能够高效地直接从树结构中获取几何信息。在初始化阶段(完成网格自适应并获取水平集函数的离散值)和求解阶段,对单元进行粗化或细化的决策均基于局部自适应准则。
软件界面
界面展示-01
界面展示-02
界面展示-03
DFCD-Plasma技术特点
DFCD-Plasma是为数值分析半导体工艺步骤对器件特征尺度的影响开发的。典型应用示例为:
-
基于水平集方法(Level Set)表征材料界面与组分通量;
- 采用自适应网格技术,实现对特征几何结构的高分辨率捕捉。
-
充分利用现有DFCD软件平台:
- DFCD-Mesh和DFCD-Poly用于几何定义;
- DFCD-Plasma基于DFCD-MultiFLOW构建;
- 输运与化学反应模型源自DFCD数据库;
- 使用DFCD-View进行可视化与结果分析。
- DFCD对工艺设备及特征尺度仿真器的统一管理,便于实现多尺度模型间的有效耦合与链接。
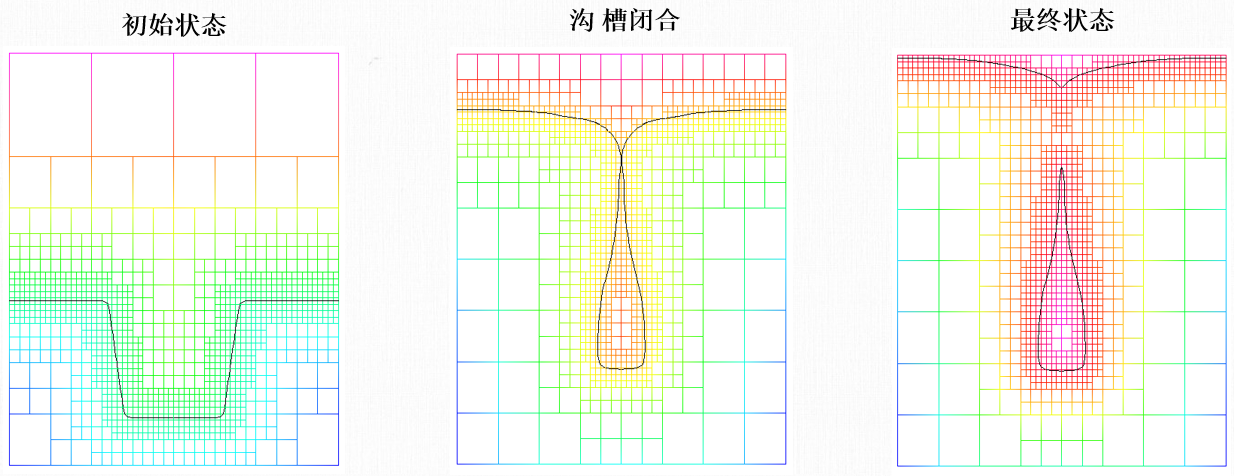
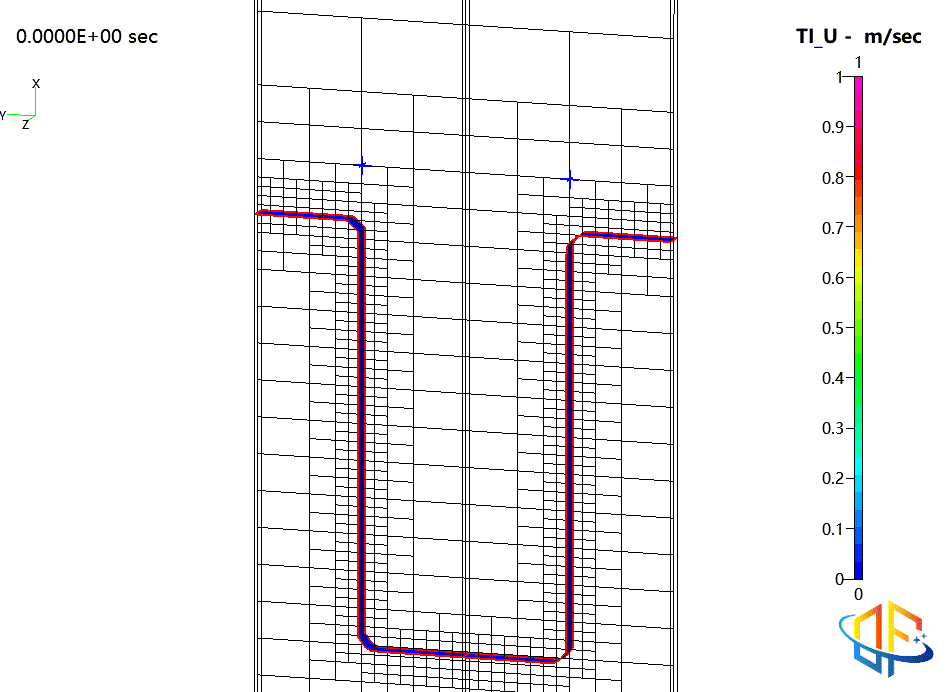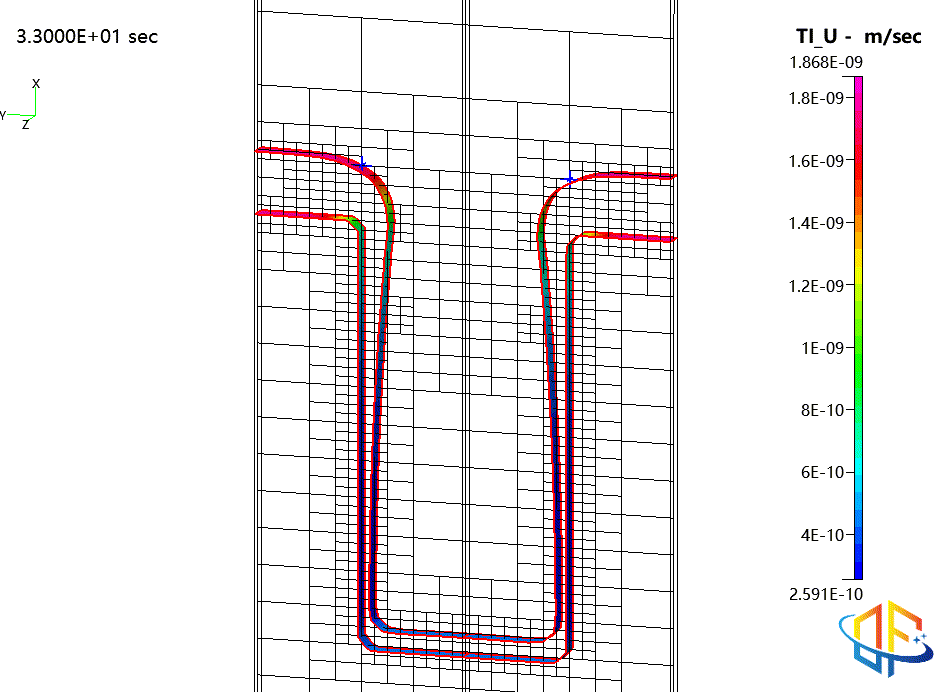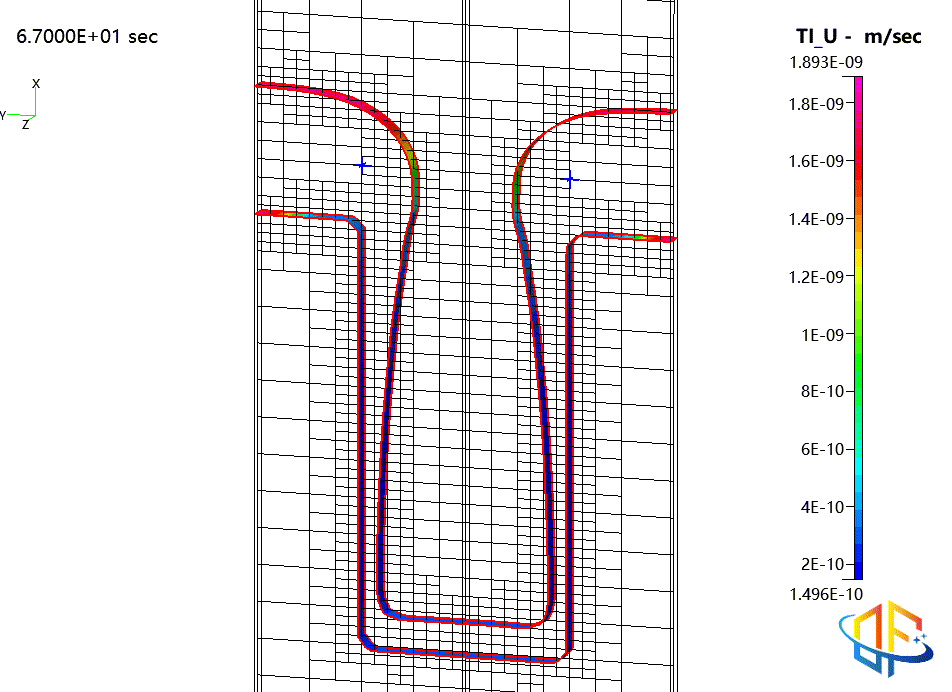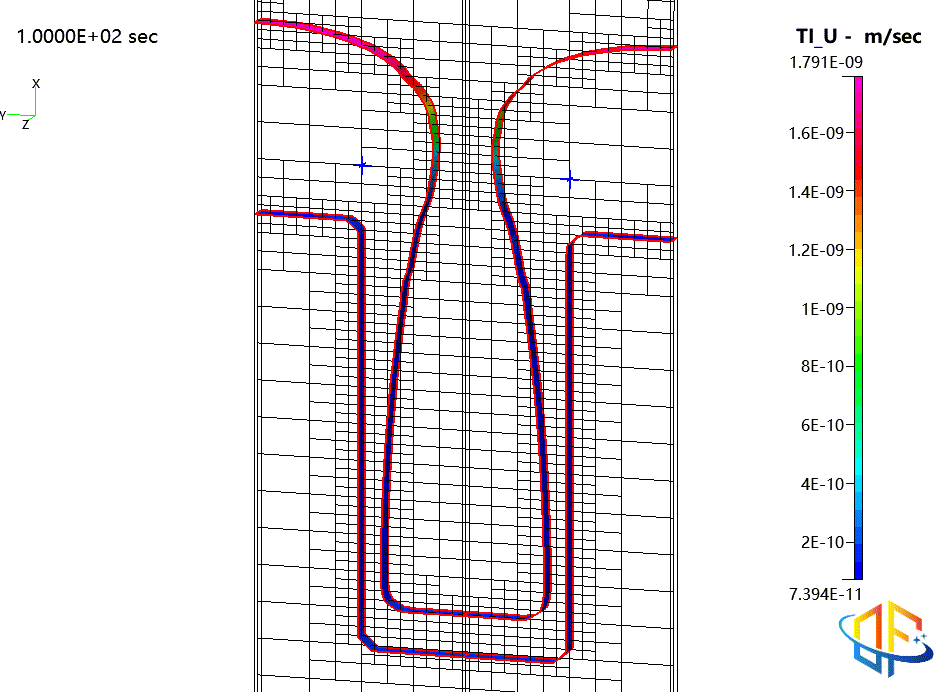
沟槽填充闭合时的求解自适应网格
基于水平集的形貌演化模型
- 水平集函数是一个标量场,其零等值面(zero isosurface)代表该函数所描述材料的边界;
- 需要借助网格对水平集函数的时间演化方程进行离散化求解;
- 可与复杂的反应机理兼容;
- 示例代码:商用软件(如 Terrain、Avanti),研究型代码(如 NASA Ames 的 SPELS),以及工业界内部代码(如 Motorola 的 ASSET);
- 缺点:无内在的质量守恒机制、需要将界面速度“延拓”到远离表面的区域、难以精确解析尖锐拐角;
- 优点:易于扩展至三维、计算速度快、可与连续介质组分输运的网格求解兼容。
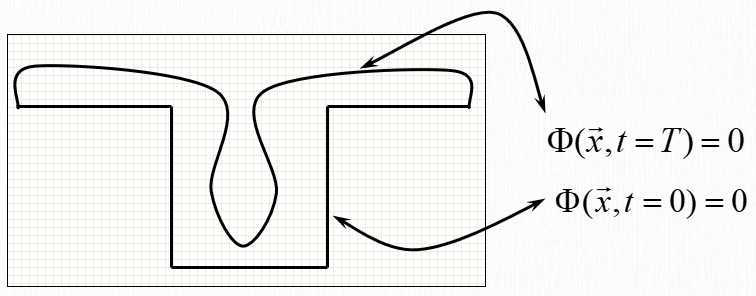
特征尺度模型
- DFCD-Plasma能够基于用户自定义输入,或基于DFCD-MultiFLOW 模拟(反应器尺度模型)生成的输入数据,精确模拟薄膜在晶圆表面沉积与刻蚀过程中形成的二维和三维形貌演化;
- 通过耦合气相组分输运与表面反应的综合效应,确定随时间变化的生长与刻蚀行为;
- 可模拟任意数量的多步表面反应,以及由化学反应引起的固体材料形状变化。
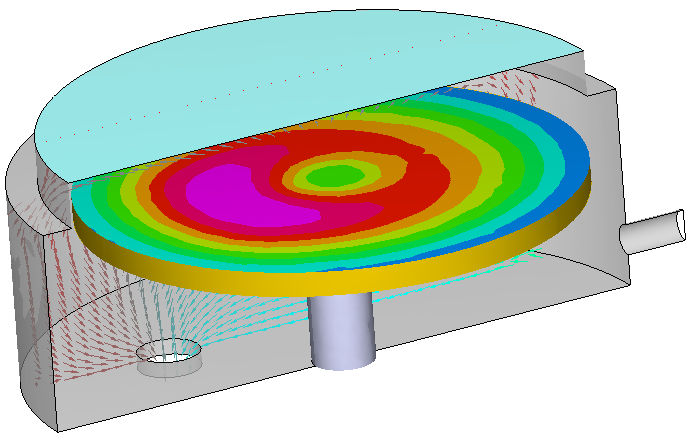
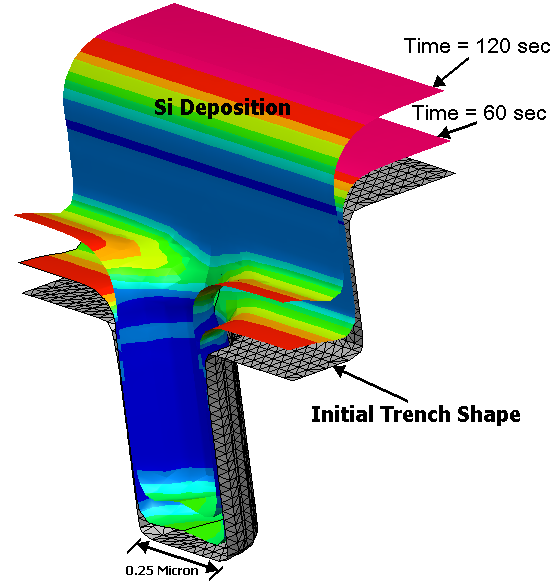
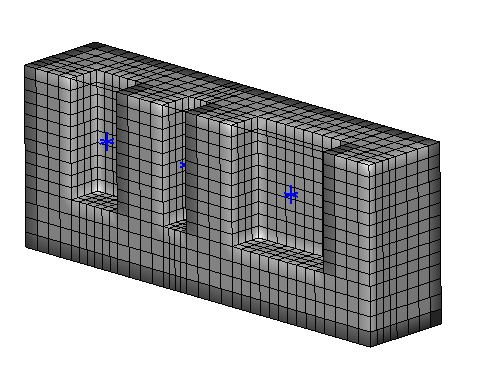

MultiFLOW和Plasma耦合
多尺度建模(Multi-scale Modelling)
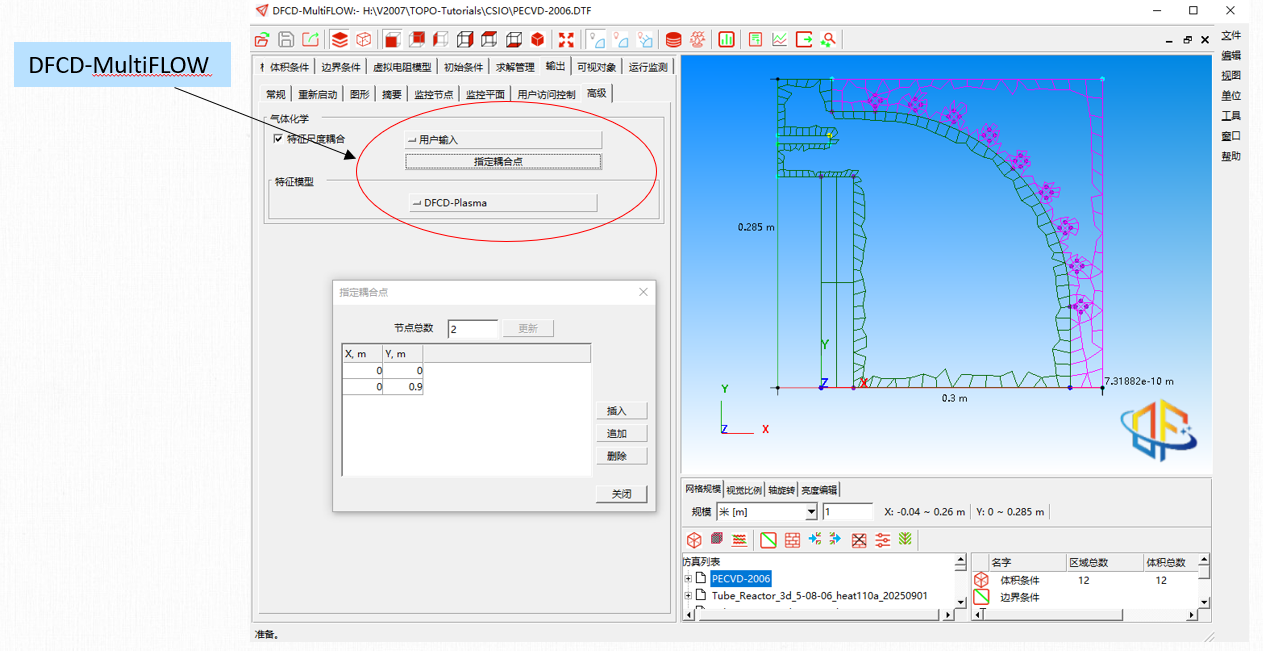
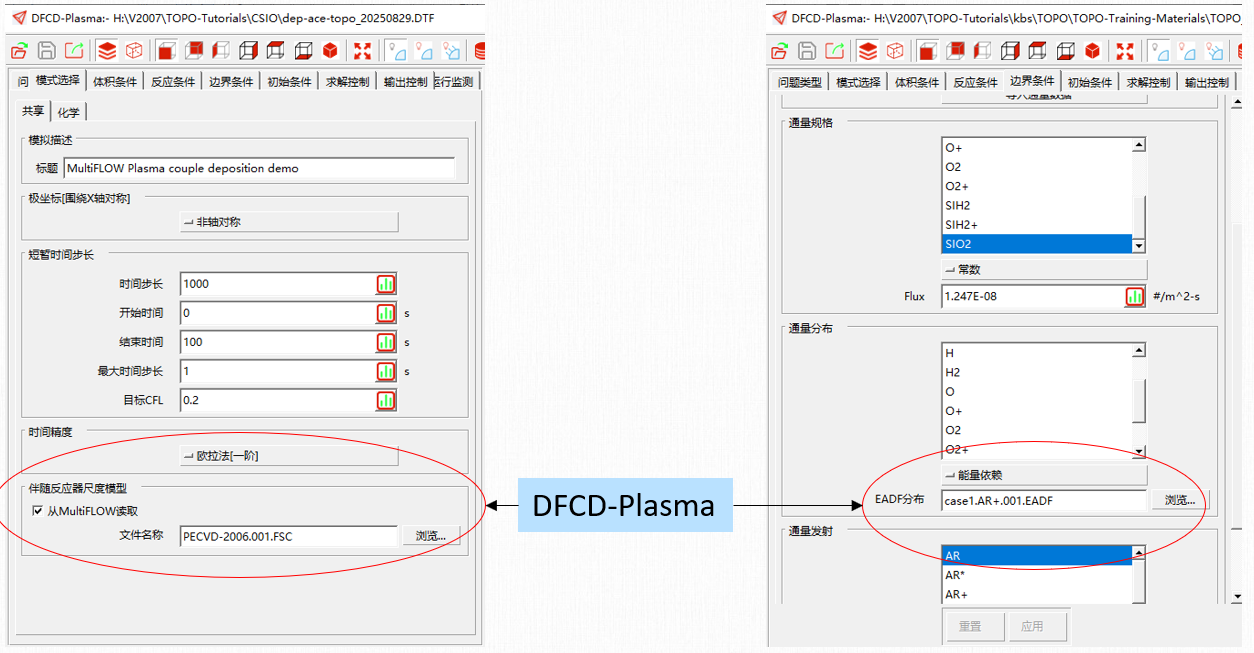
计算方法
-
提供多种离子与中性粒子通量的设定选项;
- 角度依赖的余弦分布(Cosine);
- 基于文件定义的角度依赖分布;
- 以能量和角度的查表函数形式定义的能量依赖分布。
- 支持非对称通量分布选项,用于捕捉晶圆边缘效应;
- 考虑镜面反射与漫反射行为;
- 非对称通量分布选项;
-
提供多种离子与中性粒子通量的设定方式;
- 角度依赖的余弦分布;
- 基于文件定义的角度依赖分布;
- 能量依赖分布,以能量和角度的查表函数形式给出。
- 考虑镜面反射与漫反射行为
- 组分与反应数据库;
-
精确模拟物理过程。
- 依赖离子能量的反应速率因子;
- 依赖离子能量的产额因子;
- 依赖离子角度的产额因子。
通量计算
- 在气相-固体界面处,使用移动立方体算法提取离散的表面单元;
-
采用半立方体法计算每个离散表面与其周围环境之间的视角因子;
- 同时累积来自具有方向分布的通量入口的入射通量;
- 离散化过程由用户控制;
- 为捕捉高深宽比特征结构底部的离子通量,需要极高的半立方体分辨率,导致计算耗时较长;
- 无法模拟电场导致的粒子轨迹偏转。
-
视角因子表示从表面i漫发射或漫反射的通量中,到达表面j的比例。
$$G_{ij} = g_i \cdot A_i \cdot F_{ij} / A_j$$
通量射线追踪法
- 通量从“入口”以指定的角度分布发射,可实现更优的采样效果和更高效的积分计算;
- 算法设计支持扩展至粒子碰撞和轨迹偏转(如电场作用下的弯曲)模拟。
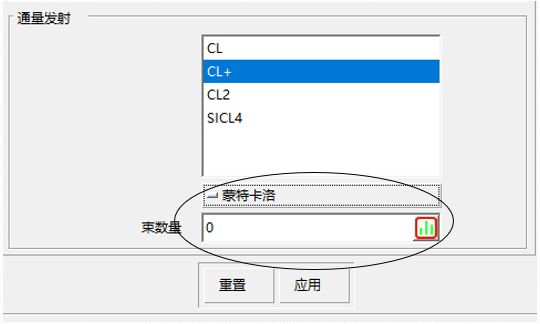
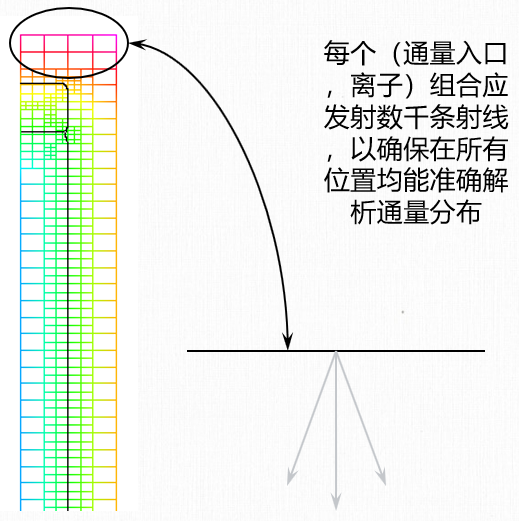
具有镜面反射的通量
- 在求解反应-通量平衡过程中,镜面反射产生的通量不能被表面反应直接消耗;
- 镜面反射的角度分辨率等同于半立方体分辨率(立体角与像素尺寸成正比);
- 在每次通量-反应迭代中,所追踪的最大镜面“反弹”次数等于当前迭代次数,例如在第10次迭代时最多追踪10次反弹。
应用实例
刻蚀
- 针对两种不同材料的刻蚀模型,每种材料具有独立的反应机理;
- 离子在光刻胶表面以掠射角发生镜面反射(类镜面反射);
- 未反射的离子通量以吸附系数为1进行线性刻蚀;
- 在光刻胶-硅交界处,由于额外的反射离子通量作用,形成更深的沟槽。
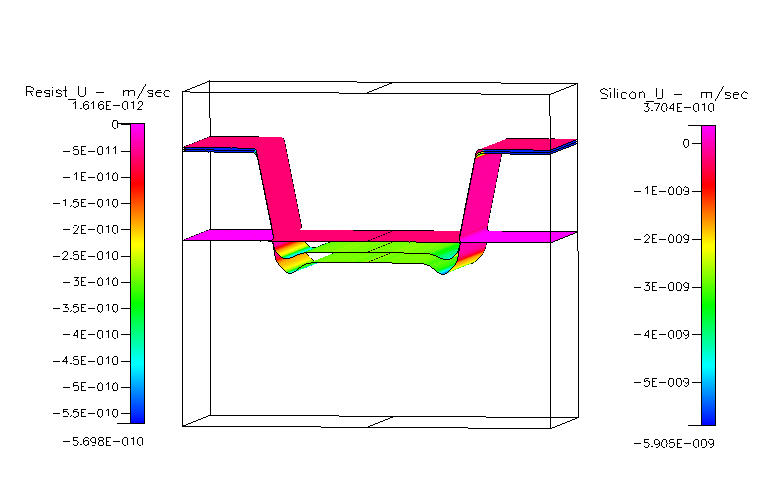
- 中性粒子/离子通量比 = 100,平均离子能量 200 eV;
- 离子角度分布为 \( \cos^{64}(\theta) \);
- 光刻胶上的 Cl⁺ 镜面反射率由角度依赖性刻蚀速率曲线确定;
- 刻蚀时间 20 秒。

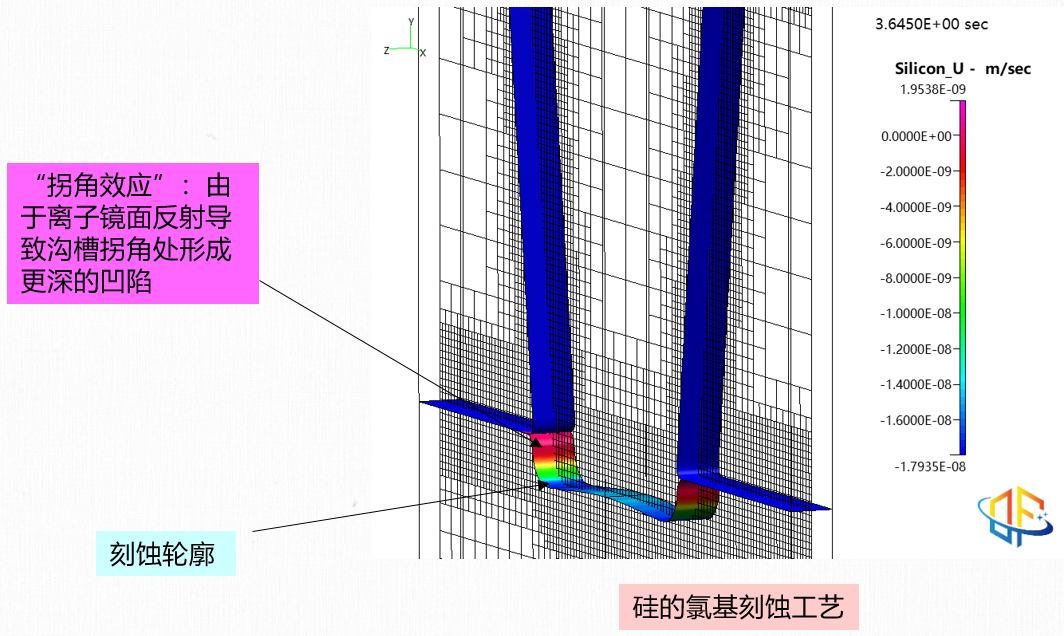
“拐角效应”:由于离子的镜面反射,在拐角处形成更深的沟槽
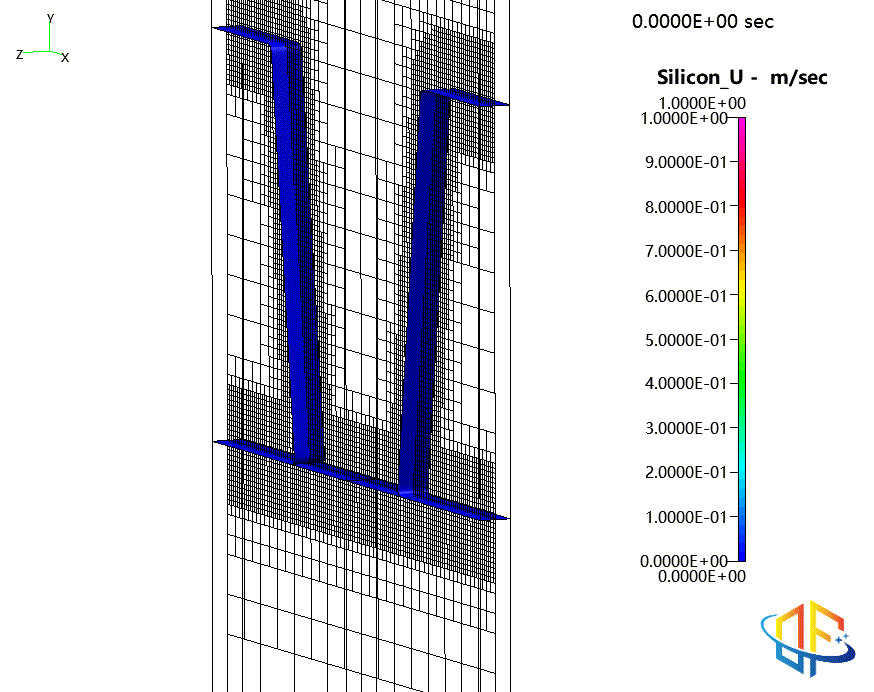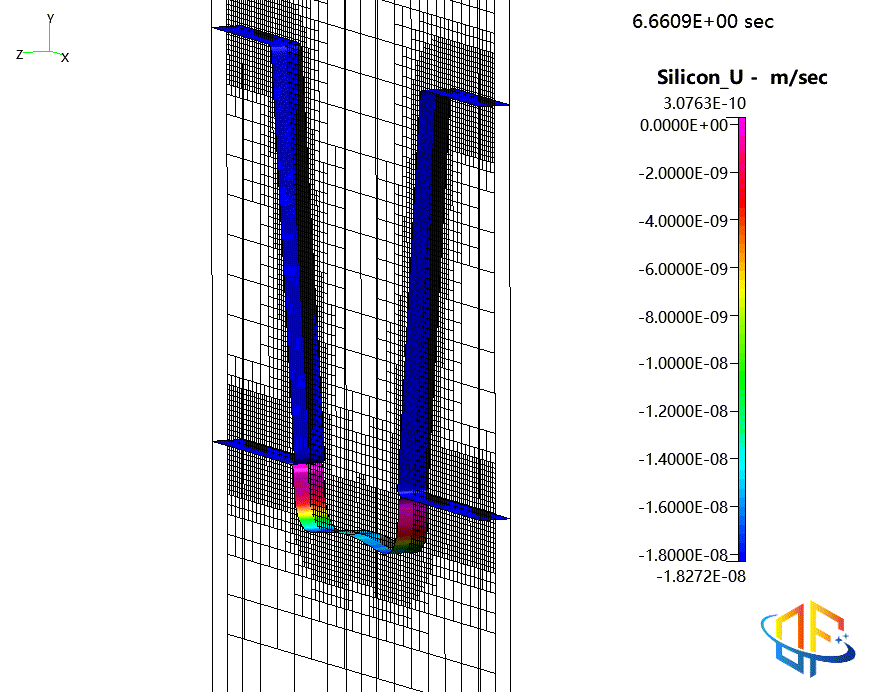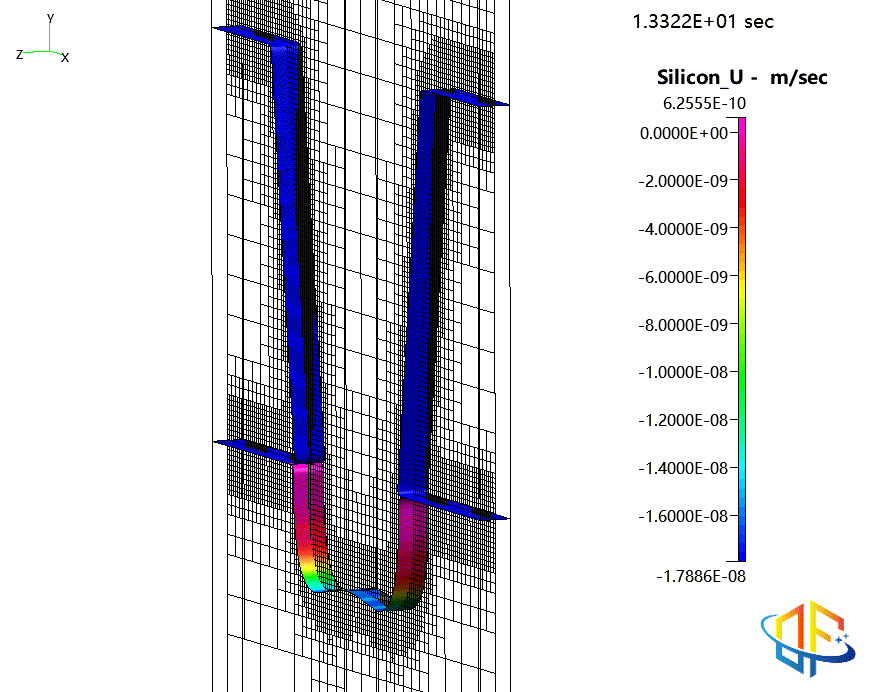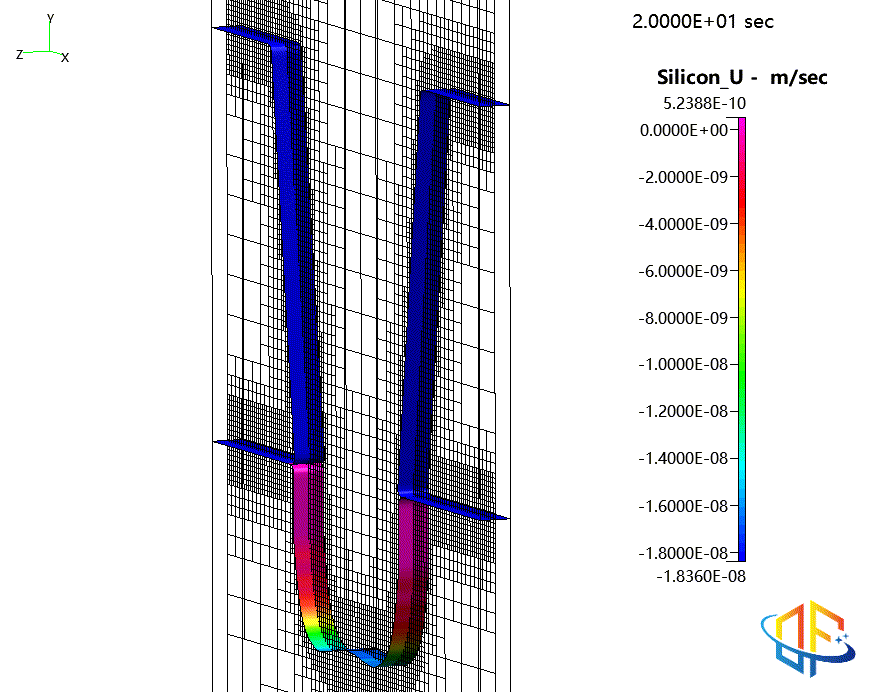

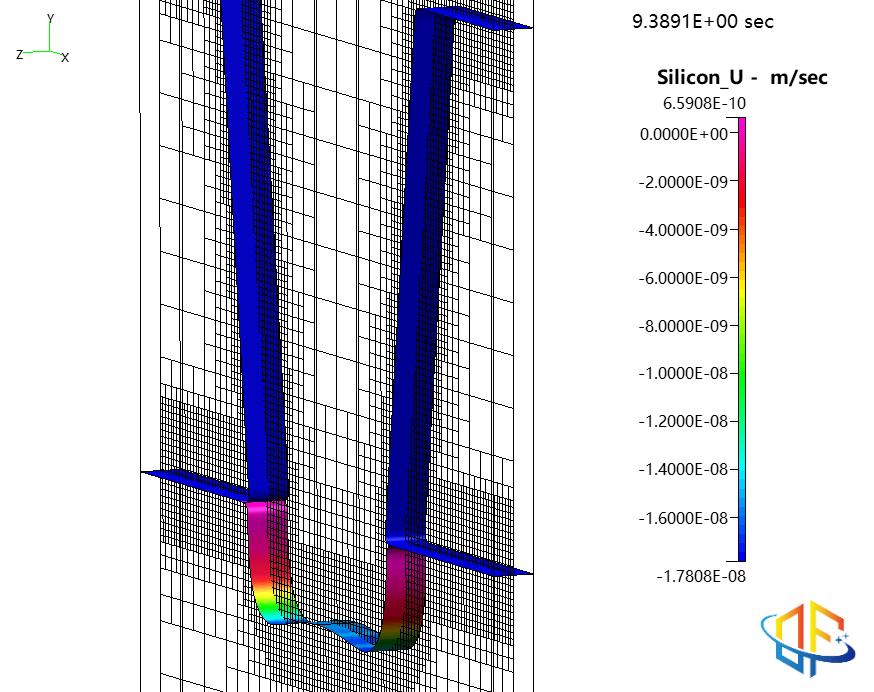
氧化物与光刻胶表面随时间的演化,按刻蚀速率着色含聚合物形成的二氧化硅刻蚀过程
物理气相沉积
钨的物理气相沉积(PVD)
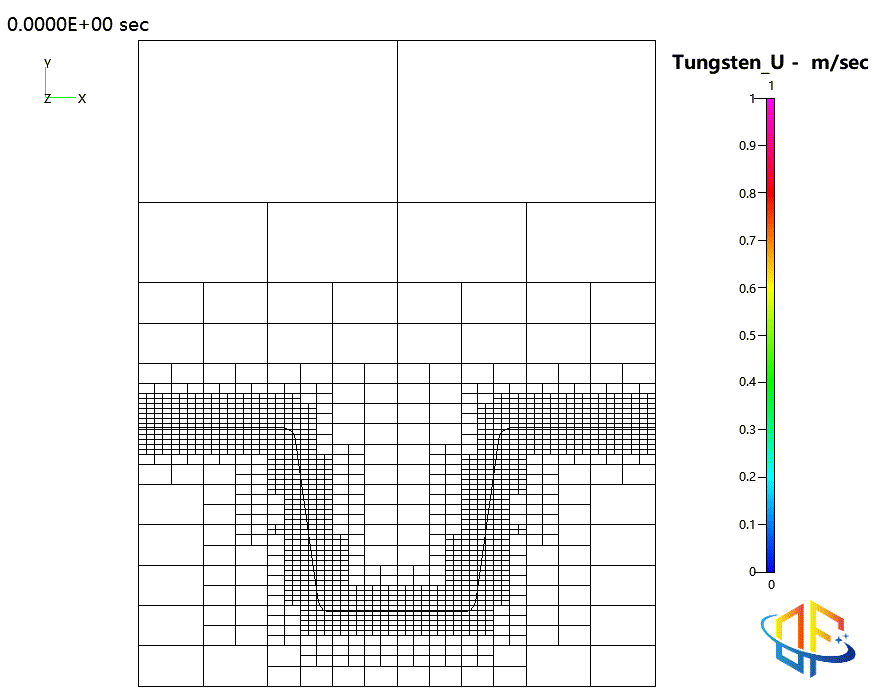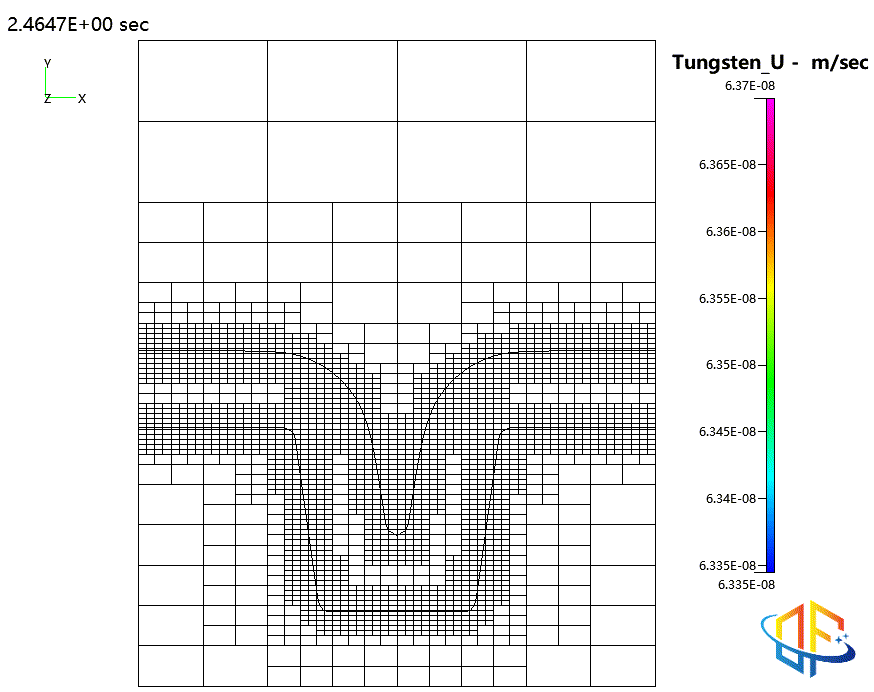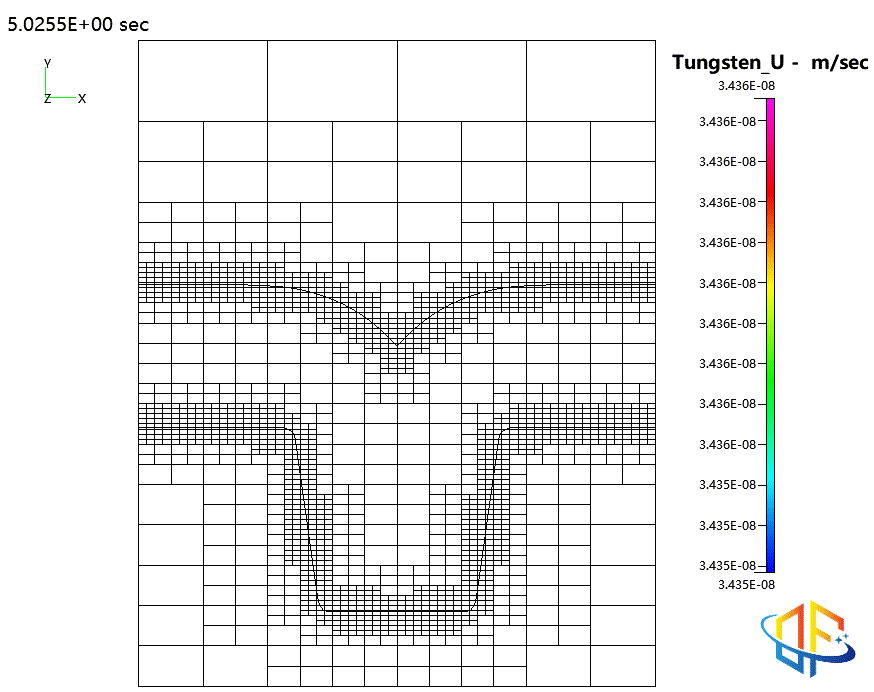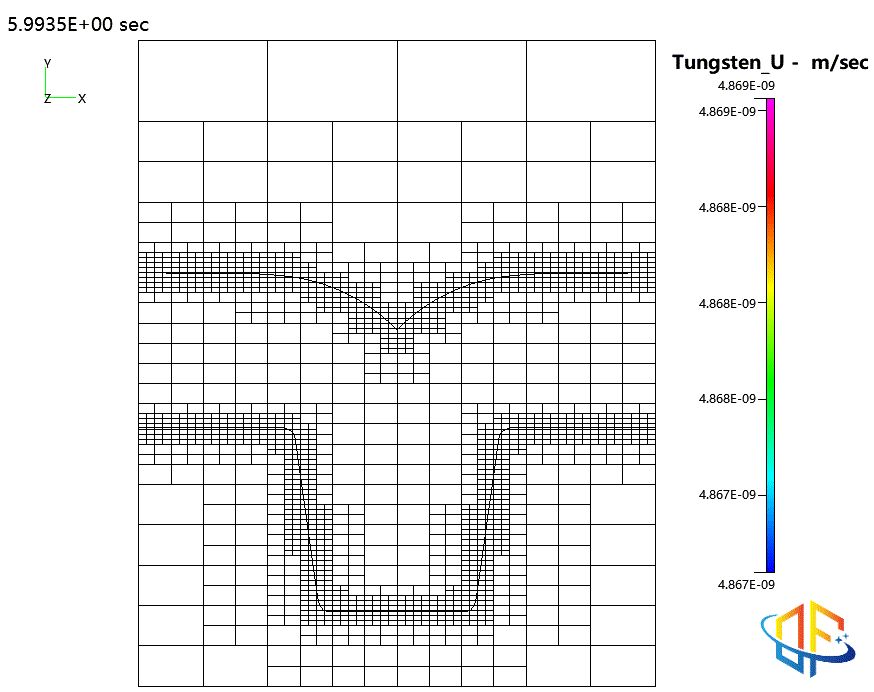
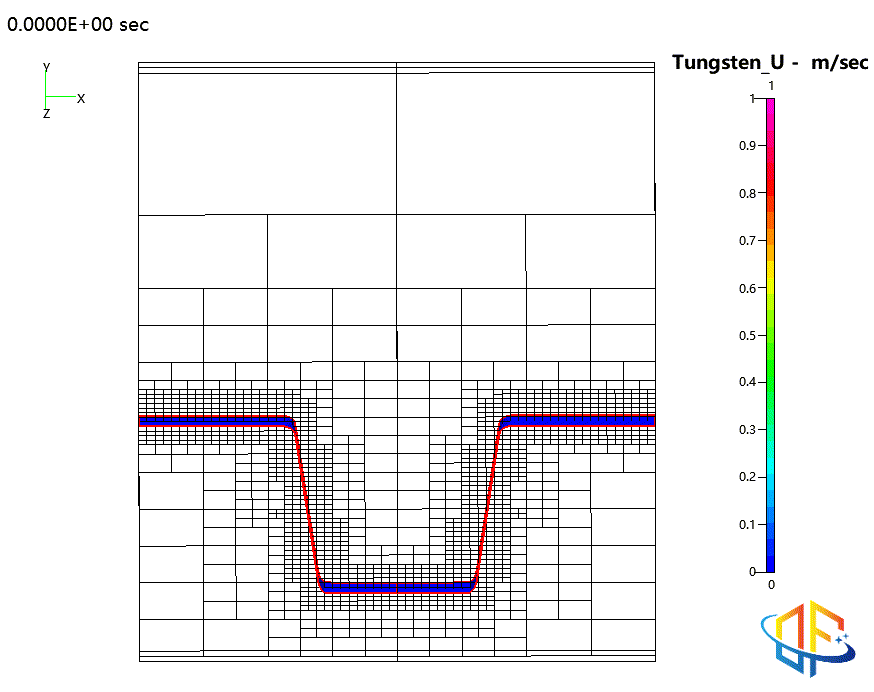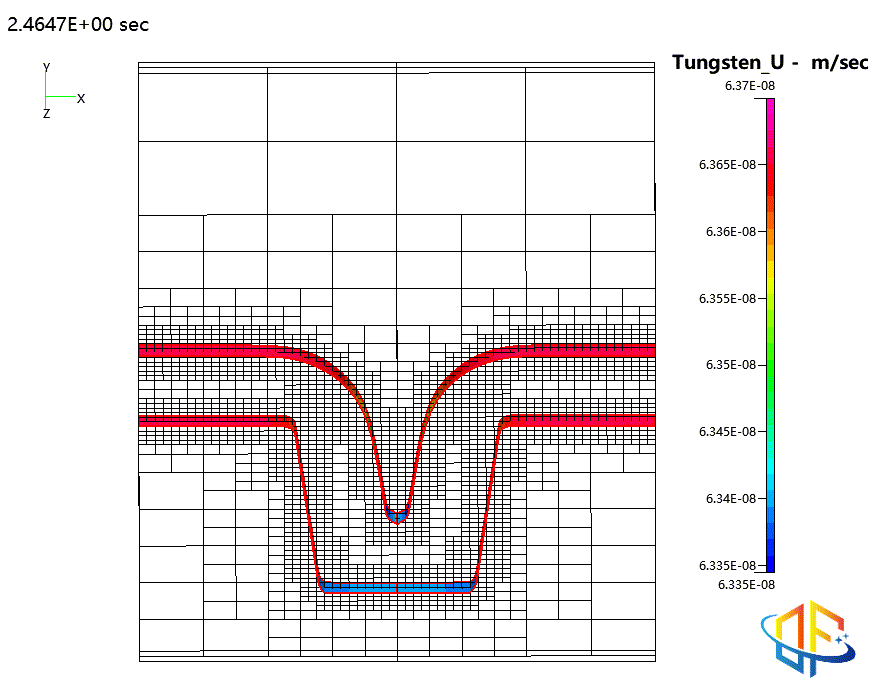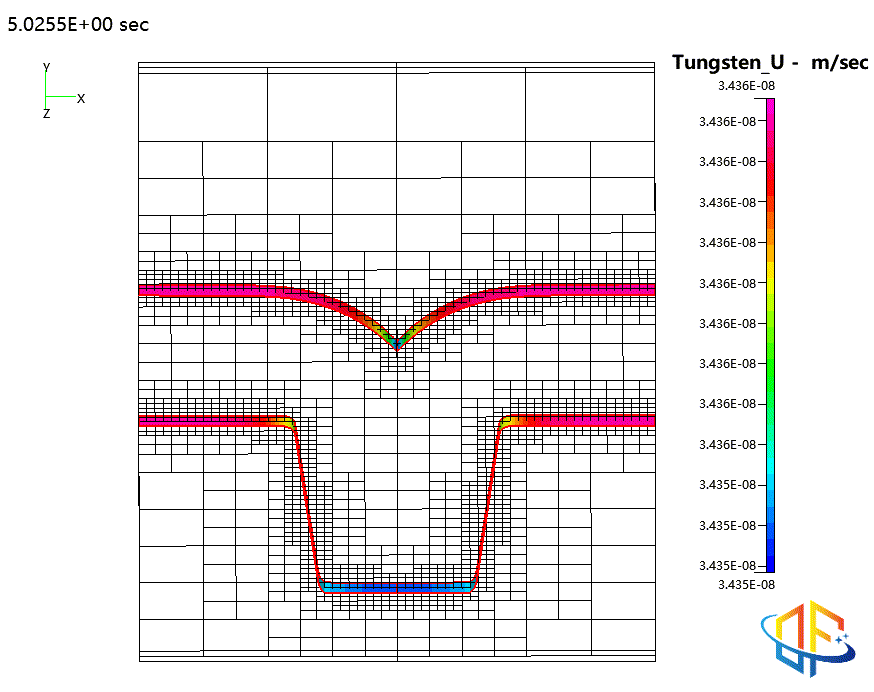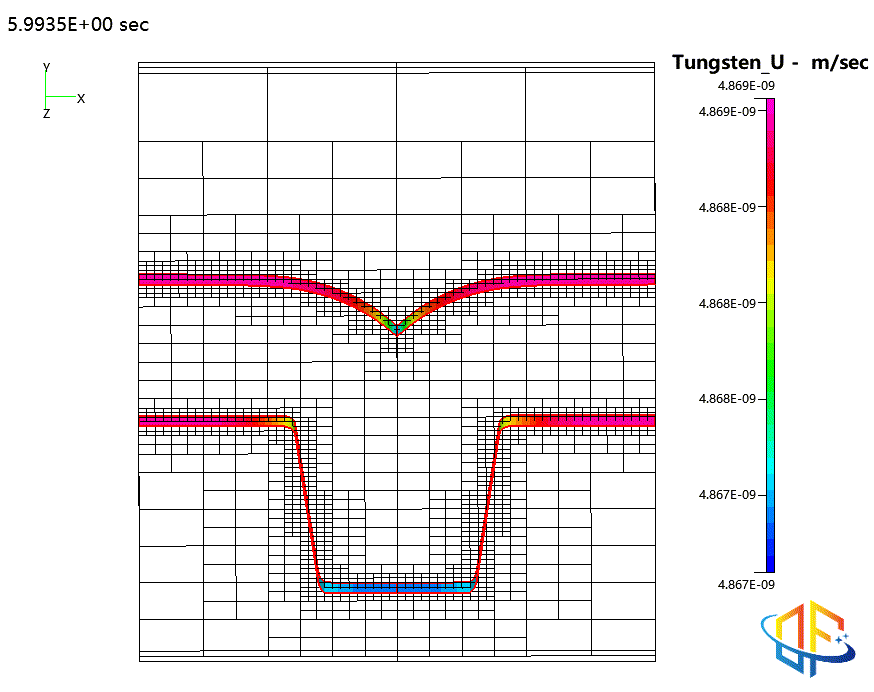
原子层沉积
钨的物理气相沉积(PVD)
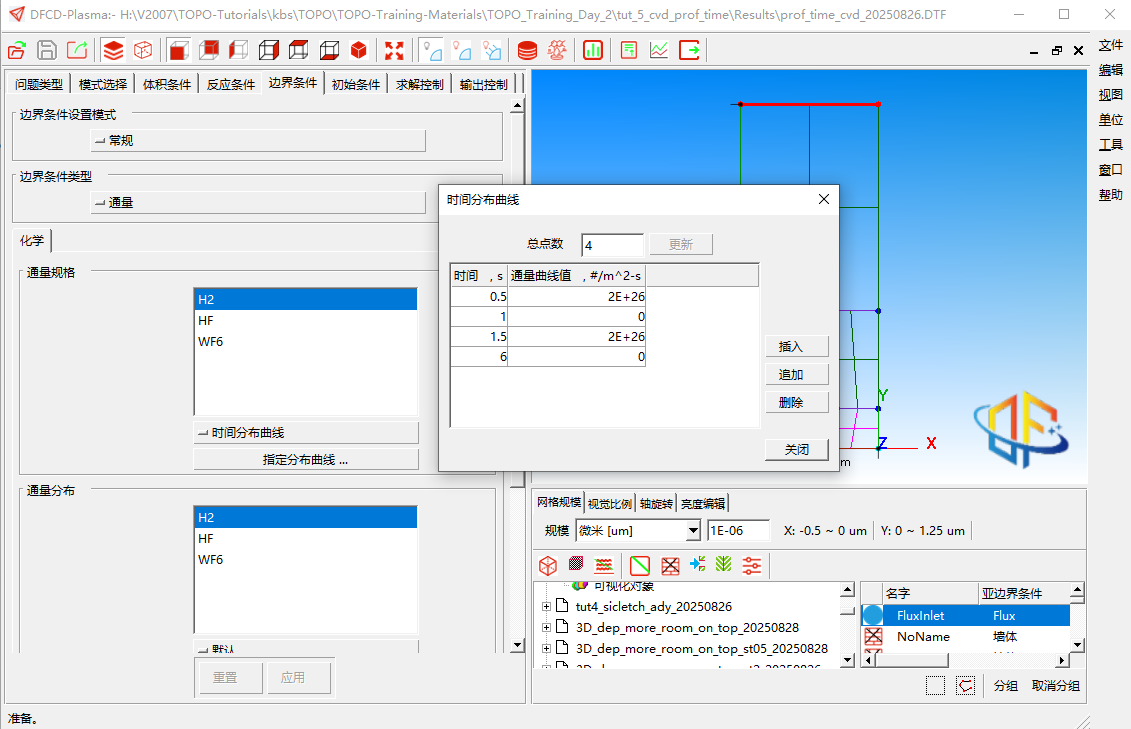
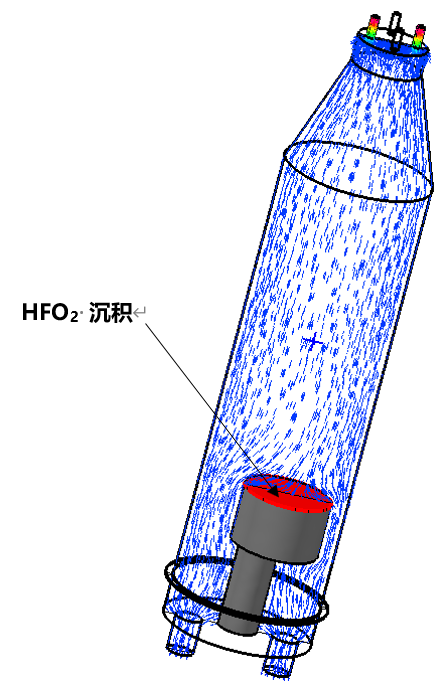
表面化学模型与脉冲组分通量选项共同实现了每个ALD循环中所需的“互补性”与“自限制性”过程
